Audio spektrogram pod linuxom

Dnešný zápis bude o softvéri pre generovanie / prehliadanie spektrogramov. Zápis samozrejme skončí ako vždy naprogramovaním vlastného skriptu :)

Open source riešenia

Nie, nie som jediný človek, ktorý chcel vidieť spektrogram. Preto existuje mnoho open source nástrojov. Niektoré z nich predstavím.

sox

Nástroj sox je konzolová aplikácia určená pre spracovanie a analýzu zvukových súborov. Spektrogram k audio súboru sa dá vygenerovať príkazom sox vstup.wav -n spectrogram.

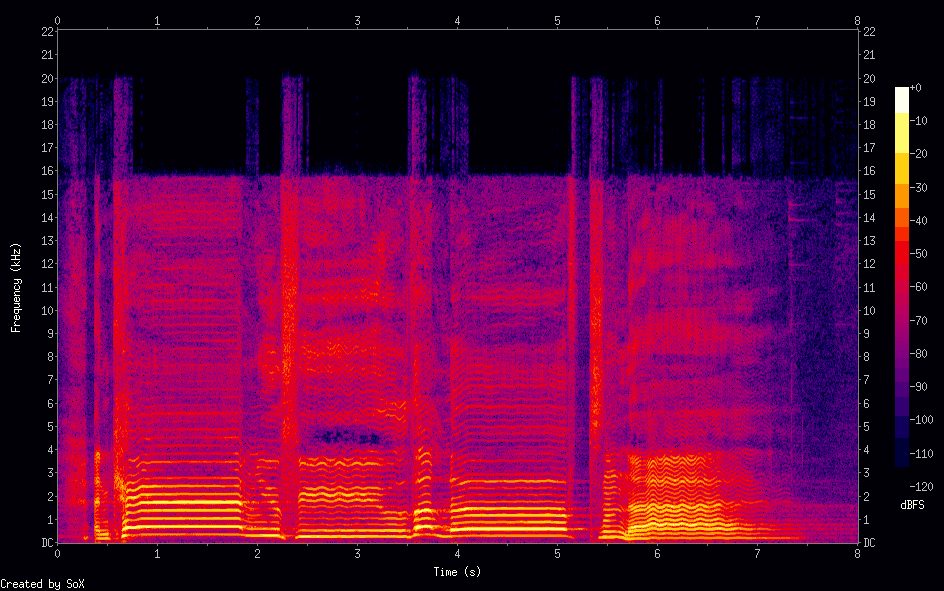
Nastaviť sa dá farba spektrogramu, rozmery, či niektoré parametre ako window fungukcia. Nasledujúci obrázok je vygenerovaný príkazom sox vstup.wav -n spectrogram -x 500 -h.

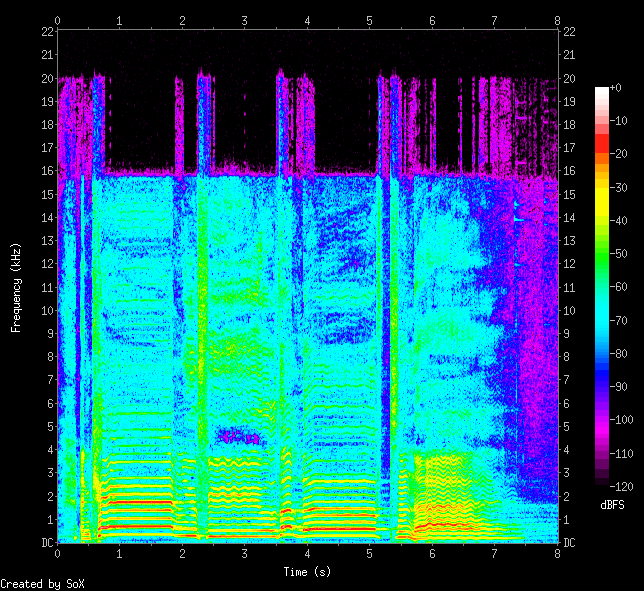
baudline

Tento nástroj je pekným rýchlym realtime analyzátorom. Rozhranie je na môj vkus dosť šialené, ale nič, na čo by sa nedalo zvyknúť.

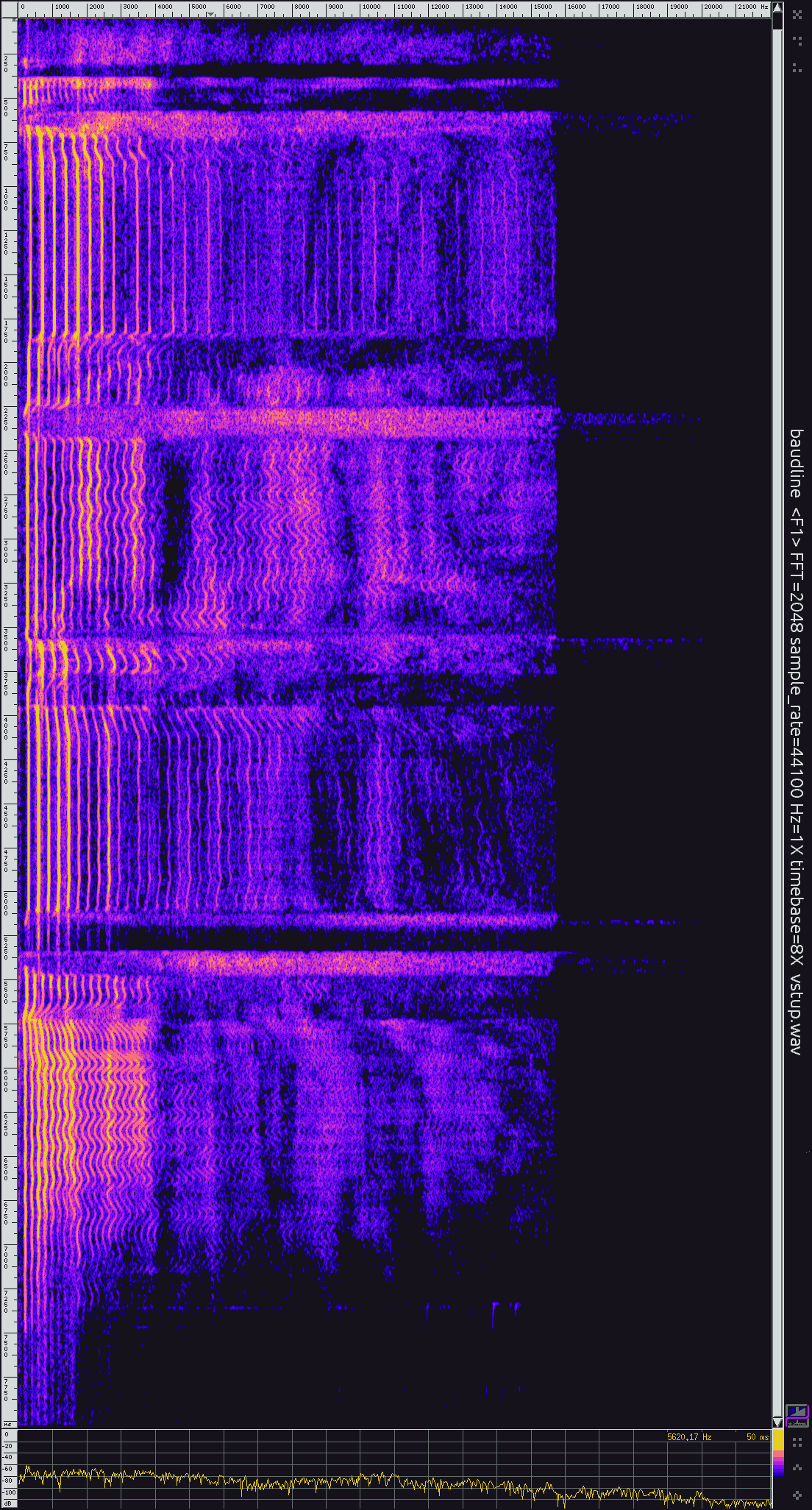
spek

Tento nástroj vie zobraziť spektrogram. Jeden konkrétny typ bez možnosti zmeniť farby, alebo čokoľvek ovplyvniť.

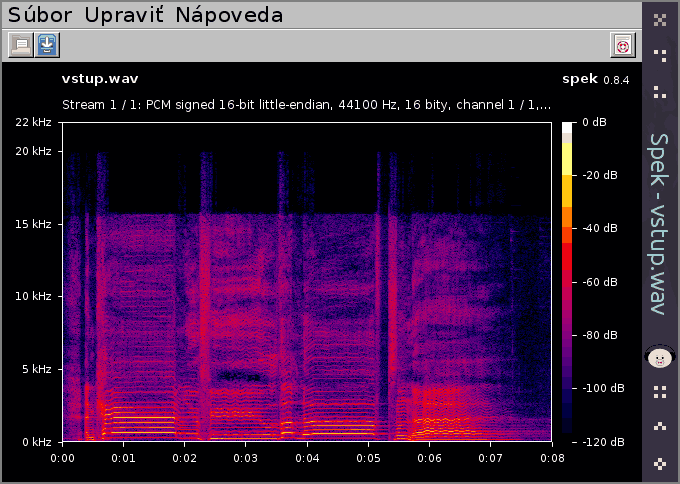
Kde je problém?

Hlavný problém, na ktorý som narazil u všetkých projektov je lineárne mierka pre frekvencie. Najdôležitejšie spektrálne čiary sú sústredené do frekvencie 1 kHz, ktorá je sotva viditeľná.

Vlastný nástroj

Keďže som vážne nenašiel nič použiteľné, rozhodol som sa napísať vlastný malý nástroj. Výber padol ako obyčajne na pythone s použitím funkcie stft z balíka scipy. Závislosti budú obmedzené na numpy (numerické výpočty), scipy (spracovanie signálov) a matplotlib (vykreslenie výsledkov).

Podpora vstupných formátov

Medzi závislosťami som neuviedol žiadnu knižnicu na načítanie multimediálnych súborov. Pri podpore súborov sa nechcem uspokojiť s ničím menším než so všetkým, čo podporuje ffmpeg. Namiesto použitia knižnice ale používam priamo binárku ffmpeg a ffprobe. Teraz sa budem chvíľu zaoberať malými ulitlity funkciami. Najskôr definujem šablóny pre volanie príkazov ffmpeg a ffprobe.

FFPROBE_CMDLINE = 'ffprobe {file} -print_format json -show_format -show_streams -loglevel error'
FFMPEG_CMDLINE = 'ffmpeg -i {file} {trim} -ac 1 -f s16le -vn -loglevel error -'

Do príkazov som pridal nejaké zástupné symboly - {file} pre vstupný súbor a {trim} pre orezanie vstupu. Výstupom príkazu ffmpeg bude jednokanálový prúd 16-bitových little endian hodnôt.

Pre zostavenie príkazu som pripravil funkciu build_shell_command, ktorá nahradí zástupné symboly. Funkcia nepracuje na úrovni reťazcov, ale na úrovni tokenov, čo umožňuje zostaviť príkaz bezpečnejším spôsobom - pri spustení sa bude priamo používať pole argumentov namiesto reťazca, takže sa nemôže stať, aby niekto vložil do zástupného symbolu úvodzovky, bodkočiarku, čo by mu umožnilo spustiť vlastný príkaz.

Token je možné nahradiť hodnotou:

• None - token sa odstráni
• reťazec - token sa nahradí reťazcom
• pole - na mieste tokenu sa vloží niekoľko argumentov

Samotná funkcia vyzerá takto:

def build_shell_command(cmd, replacements):
    # Rozdelenie na tokeny
    params = shlex.split(cmd)

    # Vytvorenie poľa náhrad
    replacements = {'{'+key+'}': val for key, val in replacements.items()}

    new_params = []
    for param in params:
        # Nájdenie náhrady
        replacement = replacements.get(param, param)
        # Hodnota None odstráni token
        if replacement is None:
            continue
        elif isinstance(replacement, list):
            # Zoznam sa pripojí k existujúcim parametrom
            new_params += replacement
        else:
            # Inak sa len token nahradí hodnotou
            new_params.append(replacement)
    return new_params

K spracovaniu vstupného súboru je potrebné zistiť jeho parametre, napríklad počet samplov za sekundu. Získanie informácií nástrojom ffprobe vyzerá takto:

def get_media_info(file):
    cmd = build_shell_command(FFPROBE_CMDLINE, {'file': file})
    return json.loads(subprocess.check_output(cmd))

Analýza

Analýza audio signálu pomocou funkcie stft je pomerne jednoduchá.

fft_size = 2048 # veľkosť FFT okna
step_size = 512 # 512 samplov na pixel

frequency, time, fft = signal.stft(
    audio_data,
    audio_sample_rate,
    window=args.window,
    nperseg=fft_size,
    noverlap=fft_size - step_size
)

fft = np.abs(fft)
fft = 20.*np.log10(fft)

Zobrazenie

Analýzu signálu by sme mali za sebou, zostáva už len zobraziť výsledok. Nasledujúci kód používa matplotlib na vygenerovanie obrázka.

import matplotlib.pyplot as plt

fig = plt.figure()
ax = fig.add_subplot()

# Zobrazenie fft s minimálnym ziskom -100dB a maximom -30dB
im = ax.pcolormesh(time, frequency, fft, vmax=-30, vmin=-100, cmap='inferno', shading='gouraud')
# Nastavenie osí
ax.set_ylim(0, 8000)
ax.set_ylabel('Frequency [Hz]')
ax.set_xlabel('Time [sec]')
# Zobrazenie mriežky
ax.grid(color='#ffffff', axis='y', which='major', alpha=0.5)
ax.grid(linestyle='dotted', color='#ffffff', axis='y', which='minor', alpha=0.3)

fig.savefig("spektrogram.png")

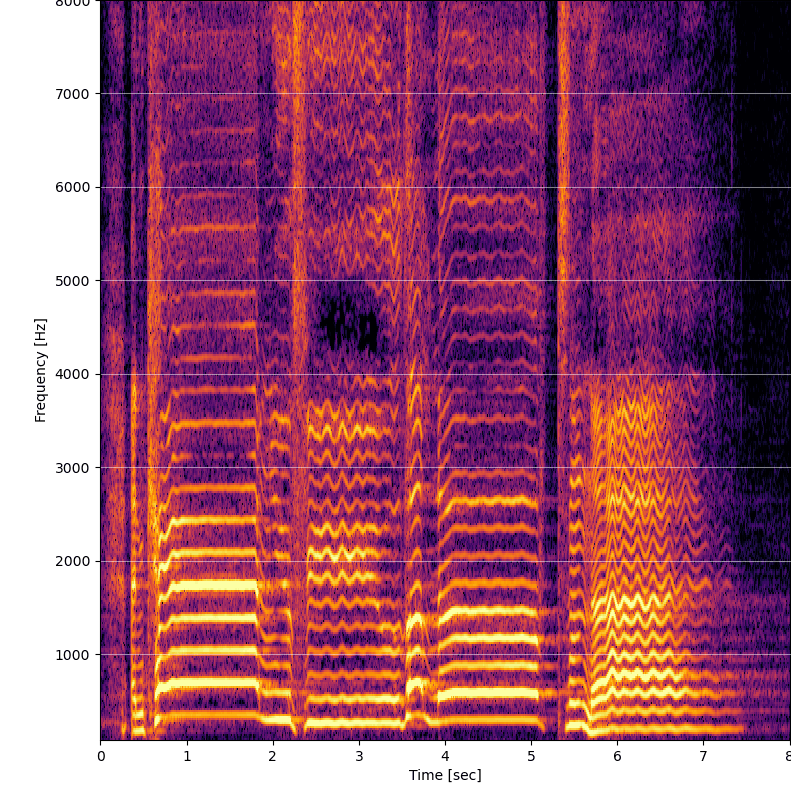
Počkať, nehovoril som niečo o logaritmickej mierke? Aha, tak pridám do zobrazenia nasledujúci riadok:

ax.set_yscale('log')
ax.set_ylim(80, 8000)

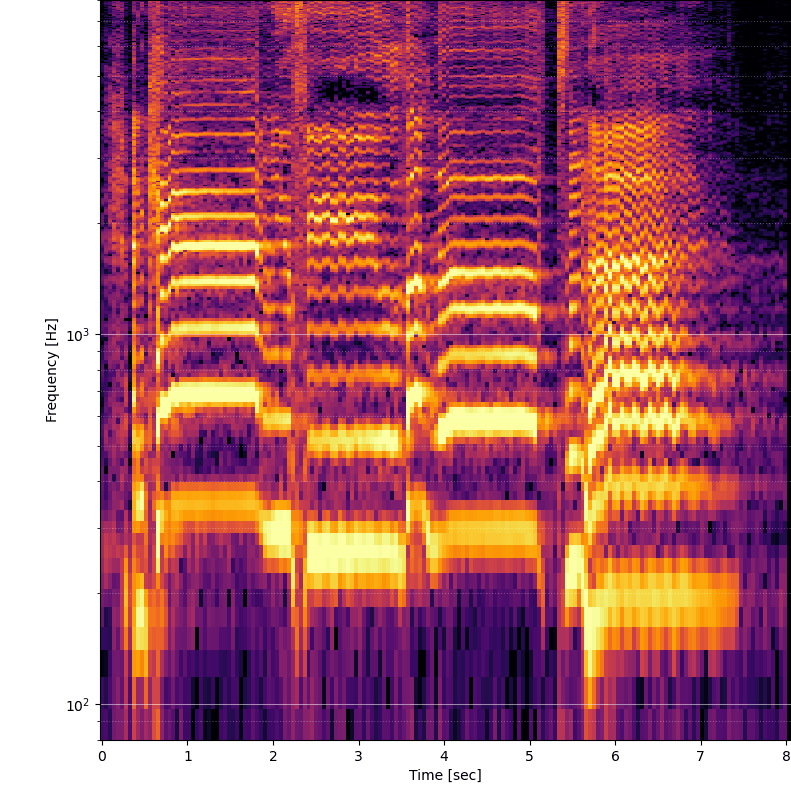
Vylepšenia

Rozlíšenie v oblasti nízkych frekvencií je mizerné. V tejto časti skúsim popísať niektoré vlastnosti rýchlej fourierovej transformácie a jej parametrov.

Dôležitým parametrom je fft_size, teda veľkosť okna fourierovej transformácie. Hodnota musí byť celou mocninou čísla 2. Čím väčšia je táto hodnota, tým viacej jemné bude zobrazenie. Napríklad ak je samplovacia frekvencia 44 100 Hz, potom výstupom rýchlej fourierovej transformácie bude rozdelenie signálu na frekvencie v rozsahu 0 - 22 050 Hz (teda polovica samplovacej frekvencie). Frekvencie budú rozdelené na rovnaké úseky, ktorých počet je polovičná veľkosť FFT okna (napríklad veľkosť okna 2048 vygeneruje 1024 frekvencíí, teda frekvencia bude delená na 21,5 Hz úseky - 22050 / 1024 = 21,5). Postačuje teda zvýšiť veľkosť okna?

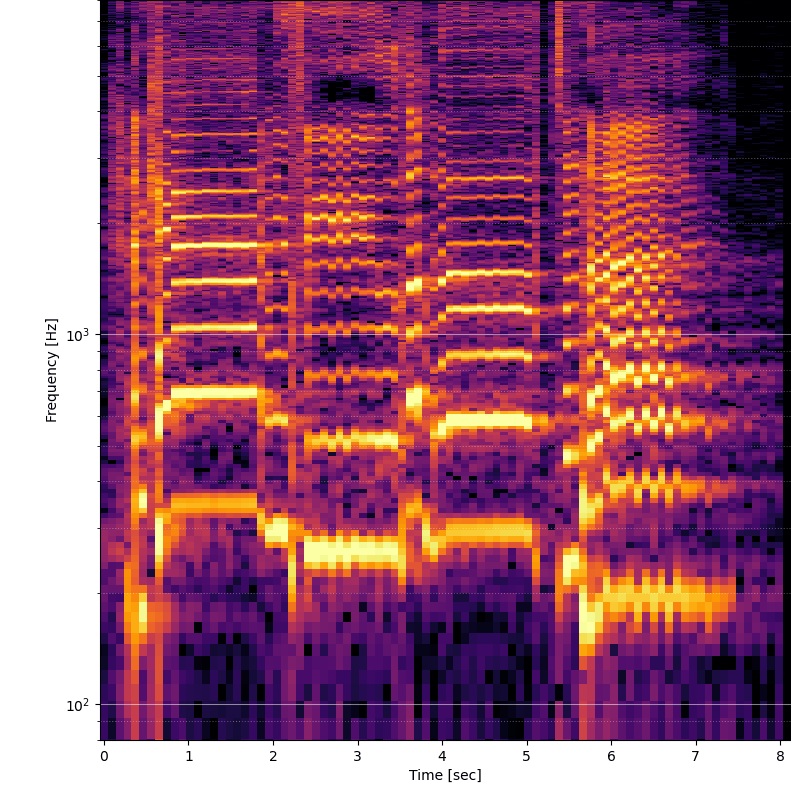
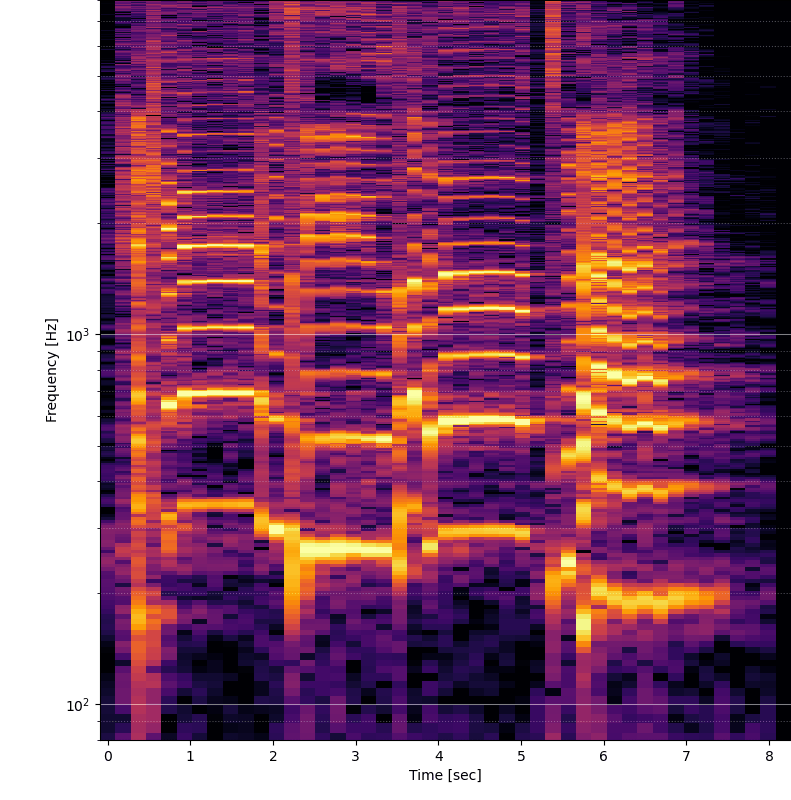
Univerzálne riešenie samozrejme neexistuje. Čím je väčšie rozlíšenie vo frekvenčnej oblasti, tým menšie je rozlíšenie v časovej oblasti. Teoretickým riešením je posúvanie okna o menšiu vzdialenosť než veľkosť okna (parameter noverlap funkcie stft).

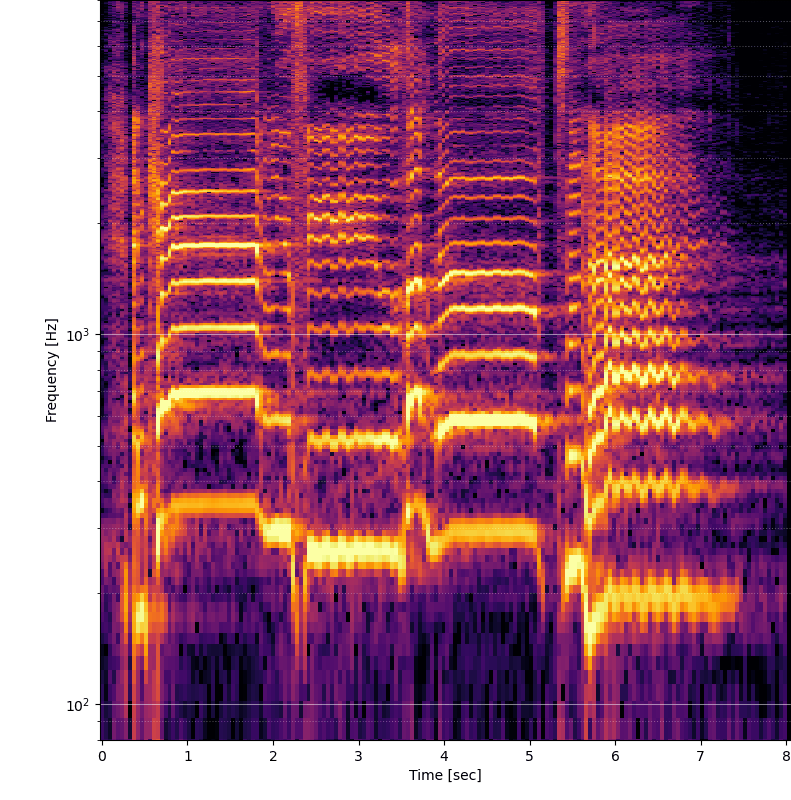
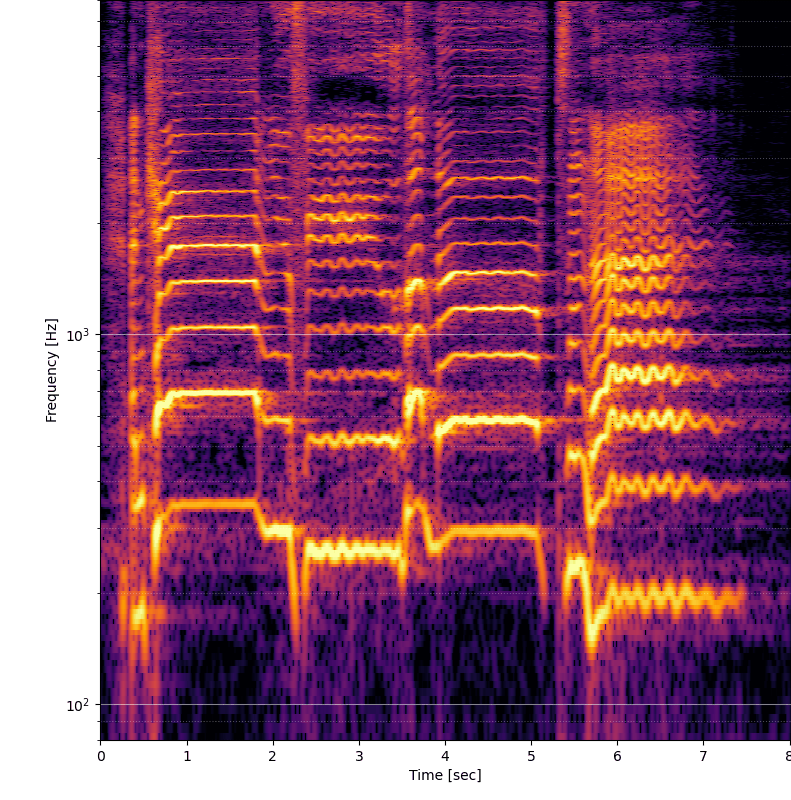
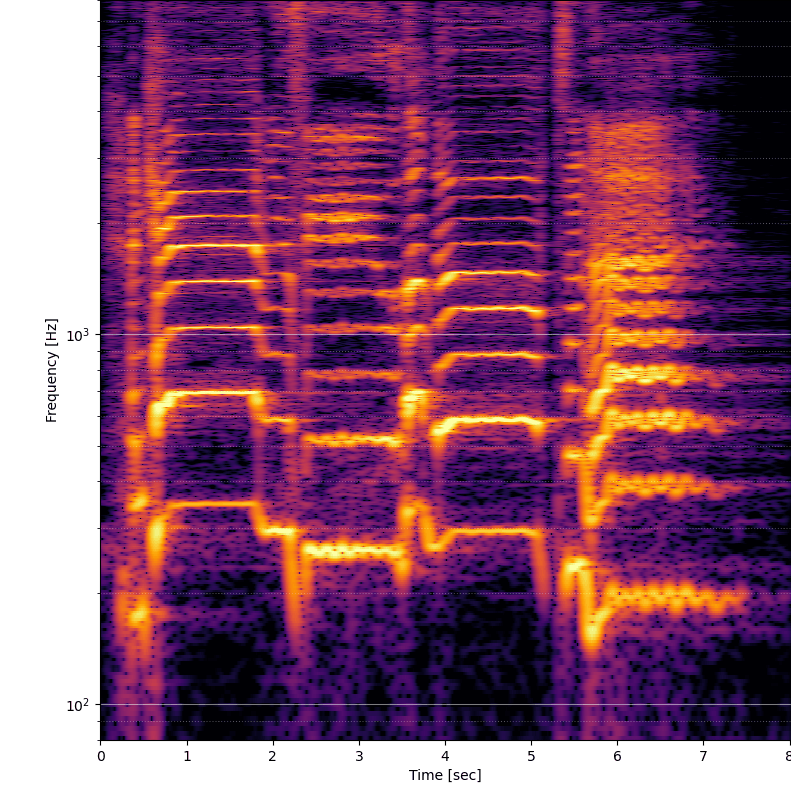
Výsledky sú podstatne lepšie, ale stále je tu problém, že pri väčšej veľkosti okna sa síce zaostria spodné frekvencie, ale na časovej osi sa signál rozostrí. Ideálne by teda bolo na vysokých frekvenciách znížiť veľkosť FFT okna a na nižších naopak používať čo najväčšie FFT okno, aby sa skombinovali výhody / nevýhody podľa oblasti.

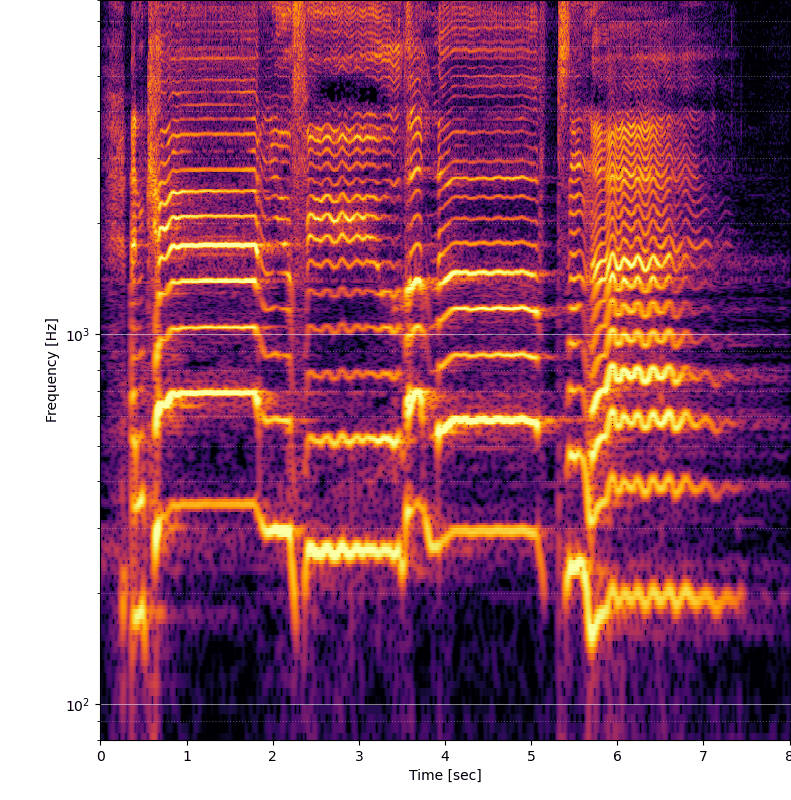
Finálny projekt

Môj malý skript som zverejnil na githube. Program podporuje rôzne parametre na nastavenie farieb, frekvencií, ziskov, škály atď. Nasledujúci obrázok je generovaný príkazom:

./spectrogram \
	vstup.wav \
	spektrogram.png \
	--grid \
	--scale \
	--colorbar \
	--colormap nipy_spectral \
	--gain_min -80 \
	--gain_max -20 \
	--step_size 256 \
	--frequency_min 100 \
	--frequency_max 10000

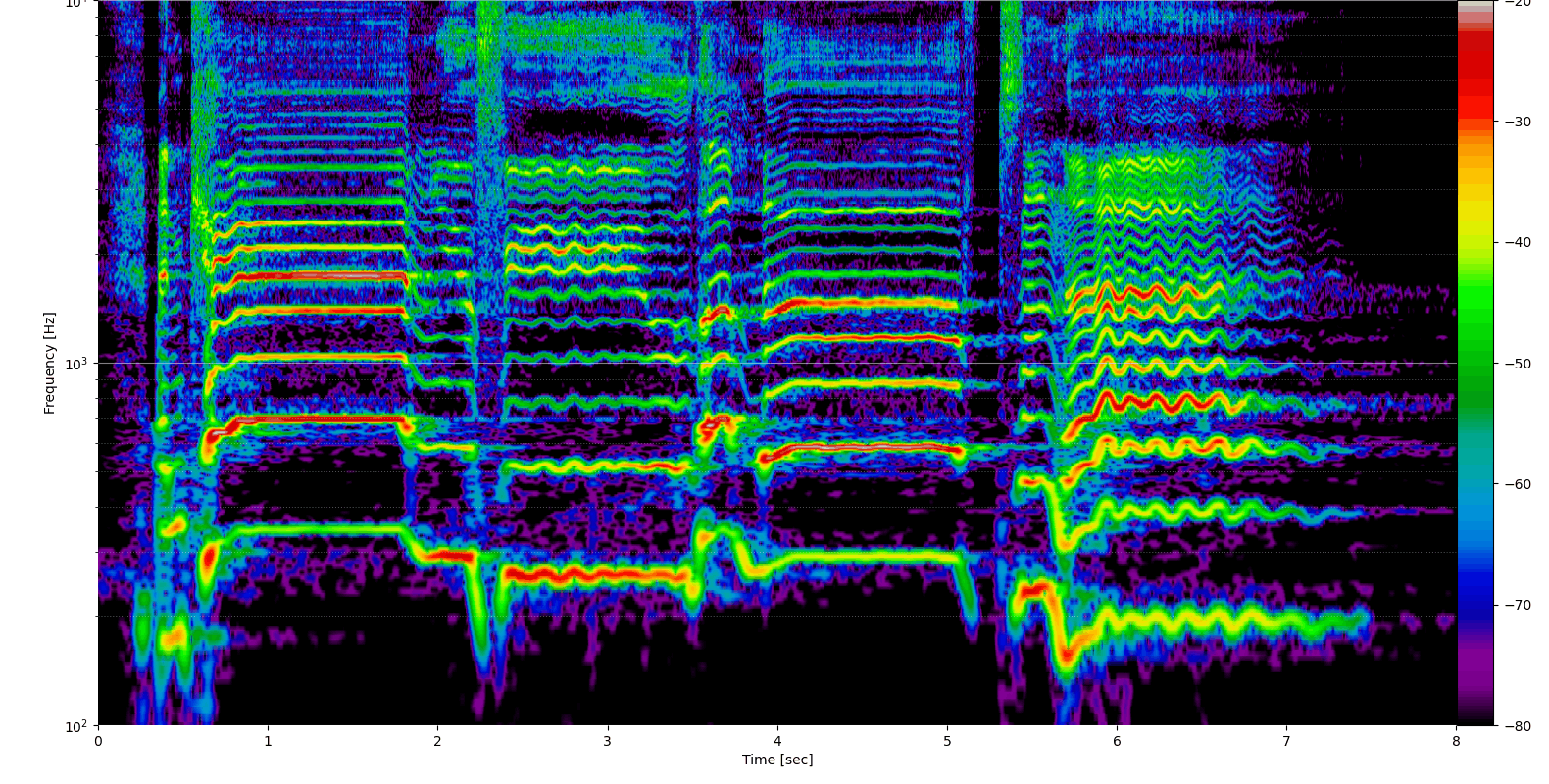
Podporované sú nasledujúce parametre:

--start

Počiatočná sekunda

--length

Dĺžka záznamu (v sekundách)

--window

Window funkcia

--colormap

Farebná mapa (z matplotlibu)

--grid

Zobraziť mriežku

--scale

Zobrazenie mierky

--colorbar

Zobrazenie colorbaru na bočnej strane

--linear

Generovanie lineárnej časovej mierky

--image_width

Šírka výsledného obrázka

--image_height

Výška výsledného obrázka

--gain_min

Minimálny zisk (štandardne -100dB)

--gain_max

Maximálny zisk (štandardne -30dB)

--frequency_min

Minimálna frekvencia (štandardne 80Hz)

--frequency_max

Maximálna frekvencia (štandardne 8 000Hz)

--step_size

Počet samplov na jeden bod na časovej osi (štandardne 512)