Shadertoy - medzi matematikou a umením (2D grafika)

11.09.2022 | 19:00 | Mirecove dristy | Miroslav Bendík

Dnešná časť seriálu o OpenGL shaderoch je venovaná vykresľovaniu 2D grafiky. V tejto časti ukážem ako vykresliť niektoré geometrické tvary, predstavím SDF funkcie, spôsob vyhladzovania (antialiasing) a vykreslenie matematických funkcií.

Kruh

Dnešnú časť začnem vykreslením kruhu, čo je najjednoduchší možný tvar na vykreslenie pomocou shaderov ak nerátam jednoliatu farbu. Príklad začnem kostrou z predchádzajúceho dielu, ktorá vykreslí prázdnu bielu plochu.

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Výpočet súradníc
    vec2 uv = fragCoord.xy / iResolution.xy;
    // Konštantný jas
    float brightness = 1.0;
    // Kombinácia jasu a alfa kanálu
    fragColor = vec4(vec3(brightness), 1.0);
}

Do pozornosti dávam konštrukciu vektora zo skaláru vec3(brightness). Tento zápis je ekvivalentný vec3(brightness, brightness, brightness).

Na začiatku súboru bude definícia polohy a polomeru kruhu. Súradnice stredu sú (0.5, 0.5), teda v strede obrazovky. Polomer je 0.4, čo bude zodpovedať 10% od okraja.

const vec2 center = vec2(0.5, 0.5);
const float radius = 0.4;

Pre každý pixel sa musí vypočítať vzdialenosť od stredu a ak je menšia než polomer, priradí sa do brightness hodnota 1.

const vec2 center = vec2(0.5, 0.5); // Súradnice stredu
const float radius = 0.4; // Polomer

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Výpočet súradníc
    vec2 uv = fragCoord.xy / iResolution.xy;
    // Výpočet vzdialenosti
    vec2 l = uv - center;
    // Jas vypočítaný zo vzdialenosti od stredu
    float brightness = step(radius, sqrt(l.x * l.x + l.y * l.y));
    // Kombinácia jasu a alfa kanálu
    fragColor = vec4(vec3(brightness), 1.0);
}

Vzdialenosť od stredu sa určí odčítaním aktuálnych súradníc od súradníc centra. Výsledkom je dvojzložkový vektor l, teda vzdialenosť od stredu na osi x a y. Veľkosť vektoru sa dá vypočítať pomocou druhej odmocniny: sqrt(l₁² + l₂² + …). Vzdialenosť stačí už len previesť na hodnotu 0 a 1 ak je veľkosť nad, alebo pod určitou hranicou. Presne na tento účel sa nám hodí funkcia step.

Výpočet veľkosti vektoru je tak často používanou funkciou, že je priamo vstavaná v jazyku GLSL pod názvom lenth. Namiesto

float brightness = step(radius, sqrt(l.x * l.x + l.y * l.y));

stačí napísať nasledujúci kód:

float brightness = step(radius, length(l));

Dokonca aj výpočet vzdialenosti je často používanou operáciou a je implementovaná v jazyku funkciou distance.

float brightness = step(radius, distance(uv, center));

Zatiaľ sa výsledok nepodobá na vyfarbený kruh. V prvom rade je vyfarbené okolie, nie samotný kruh. V podstate stačí invertovať hodnotu funkcie step odčítaním od konštanty 1.0:

float brightness = 1.0 - step(radius, distance(uv, center));

Ďalším problémom je, že „kruh“ je v skutočnosti elipsou. Dôvod je, že súradnice uv sú vždy v intervale [0, 1] aj keď pomer strán nie je 1:1. Stačí zmeniť súradnice tak, aby boli v intervale [0, 1] pre kratšiu stranu a [0, >1] pre dlhšiu stranu. Celý upravený kód vyzerá takto:

const vec2 center = vec2(0.5, 0.5);
const float radius = 0.4;

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Výpočet súradníc so zachovaním pomeru strán
    vec2 uv = fragCoord.xy / min(iResolution.x, iResolution.y);
    // Výpočet vzdialenosti
    float brightness = 1.0 - step(radius, distance(uv, center));
    // Kombinácia jasu a alfa kanálu
    fragColor = vec4(vec3(brightness), 1.0);
}

Aby bol kruh v strede, je lepšie umiestniť počiatok súradnicovej sústavy do stredu a stred kruhu sa posunie do (0, 0).

const vec2 center = vec2(0.0, 0.0);
const float radius = 0.4;

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
	// Výpočet súradníc so zachovaním pomeru strán so stredom v (0, 0)
	vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);
	// Výpočet vzdialenosti
	float brightness = 1.0 - step(radius, distance(uv, center));
	// Kombinácia jasu a alfa kanálu
	fragColor = vec4(vec3(brightness), 1.0);
}

Kruh je síce korektný, ale okraje kruhu sú zubaté. Čo tak pridať antialiasing?

Základným nápadom je využiť vzdialenosť od stredu, ale vyjadrenú v pixeloch. Pixely stačí vyplniť bielou pre polomer menší než polomer kruhu, šedou body vo vzdialenosti v intervale [polomer, polomer + 1 pixel] s úrovňou šedej rovnej vzdialenosť - polomer (v pixeloch) a čiernou v okolí. Najjednoduchšie je vyjadriť vzdialenosť v pixeloch, odrátať od nej polomer a výsledok len orezať do intervalu [0, 1]. Na orezanie poslúži vstavaná funkcia clamp.

const vec2 center = vec2(0.0, 0.0);
const float radius = 0.4;

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Výpočet súradníc so zachovaním pomeru strán so stredom v (0, 0)
    vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);
    // Koordináty * toPixelsMultiplier vráti koordináty v pixeloch
    float toPixelsMultiplier = min(iResolution.x, iResolution.y);
    // Výpočet jasu s antialiasingu
    float brightness = 1.0 - clamp((distance(uv, center) - radius) * toPixelsMultiplier, 0.0, 1.0);
    // Kombinácia jasu a alfa kanálu
    fragColor = vec4(vec3(brightness), 1.0);
}

Výsledný zdrojový kód je v súbore kruh.frag.

Modifikácia kruhu

Vykreslenie najjednoduchšieho možného útvaru nie je moc vzrušujúce. Čo tak trochu modifikovať tvar kruhu a vykresliť napríklad kvet.

Najskôr začnem definíciou konštánt ako počet okvetných lístkov, alebo ich veľkosť.

#define M_PI 3.141592654

// Stred kvetu
const vec2 center = vec2(0.0, 0.0);
// Stredný polomer okvetných lístkov
const float radius_outer = 0.4;
// Počet okvetných lístkou
const float petal_count = 7.0;
// Zmena veľkosti okvetných lístkov voči vonkajšiemu polomeru
const float petal_size_variation = 0.2;
// Polomer vnútra
const float radius_inner = 0.2;
// Vonkajšia farba (biela)
const vec4 color_outer = vec4(1.0);
// Vnútorná farba (žltá)
const vec4 color_inner = vec4(0.8, 0.8, 0.0, 1.0);

V hlavnej funkcii zatiaľ zatiaľ vykreslí jednoduchý kruh, ako v predchádzajúcom príklade s jedným malým rozdielom. Namiesto premennej brightness tu bude použitá alpha (priehľadnosť) a výstupná farba sa bude počítať ako mix pôvodnej farby a cieľovej farby s faktorom alpha.

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Výpočet súradníc so zachovaním pomeru strán so stredom v (0, 0)
    vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);
    // Koordináty * to_pixels_multiplier vráti koordináty v pixeloch
    float to_pixels_multiplier = min(iResolution.x, iResolution.y);

    float alpha = 1.0 - clamp((distance(uv, center) - radius_outer) * to_pixels_multiplier, 0.0, 1.0);
    fragColor = mix(fragColor, color_outer, alpha);
}

Vykreslenie vnútorného kruhu je vcelku triviálne. Stačí skopírovať kód pre vykreslenie vonkajšieho kruhu. Pozor, vnútorný kruh sa musí vykresliť až po vonkajšom, inak by ho vonkajší prekryl.

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
	// Výpočet súradníc so zachovaním pomeru strán so stredom v (0, 0)
	vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);
	// Koordináty * to_pixels_multiplier vráti koordináty v pixeloch
	float to_pixels_multiplier = min(iResolution.x, iResolution.y);

	// Vonkajší kruh
	float pixel_center_distance = distance(uv, center) - radius_outer;
	float alpha = 1.0 - clamp(pixel_center_distance * to_pixels_multiplier, 0.0, 1.0);
	fragColor = mix(fragColor, color_outer, alpha);

	// Vnútorný kruh
	pixel_center_distance = distance(uv, center) - radius_inner;
	alpha = 1.0 - clamp(to_pixels_multiplier * pixel_center_distance, 0.0, 1.0);
	fragColor = mix(fragColor, color_inner, alpha);
}

Vykreslenie lupeňov by mohlo byť realizované napríklad periodickou zmenou polomeru. Jednou z pekne vyzerajúcich hladkých periodických funkcií, ktoré ma napádajú je napríklad sínus.

Funkcia sínus nadobúda hodnoty v rozsahu [-1, 1]. Vhodnejší bude iný rozsah. Preto som definoval petal_size_variation, ktorá bude slúžiť na zmenšenie sínusu do rozsahu [-0.2, 0.2]. K tomu sa priráta hodnota 1, čím sa rozsah posunie na [0.8, 1.2], ktorým sa už dá bez problémov násobiť polomer. Výsledkom bude meniaci sa polomer od -20% po +20% strednej hodnoty.

Zostáva už len zistiť odkiaľ zobrať uhol pre sínus. Keďže by sa lupene mali vyskytovať pravidelne okolo stredu, bude najlepšie za hodnotu zobrať uhol ktorý zviera žiadaný pixel od stredu (funkcia atan).

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
	// Výpočet súradníc so zachovaním pomeru strán so stredom v (0, 0)
	vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);
	// Koordináty * to_pixels_multiplier vráti koordináty v pixeloch
	float to_pixels_multiplier = min(iResolution.x, iResolution.y);

	// Vonkajší kruh
	vec2 pixel_direction =uv - center;
	// Uhol medzi stredom a pixelom
	float pixel_angle = atan(pixel_direction.x, pixel_direction.y);
	// Zmena polomeru
	float radius = radius_outer * (1.0 + petal_size_variation * sin(petal_count * pixel_angle));
	float pixel_center_distance = distance(uv, center) - radius;
	float alpha = 1.0 - clamp(pixel_center_distance * to_pixels_multiplier, 0.0, 1.0);
	fragColor = mix(fragColor, color_outer, alpha);

	// Vnútorný kruh
	pixel_center_distance = distance(uv, center) - radius_inner;
	alpha = 1.0 - clamp(to_pixels_multiplier * pixel_center_distance, 0.0, 1.0);
	fragColor = mix(fragColor, color_inner, alpha);
}

Celý zdrojový kód je dostupný na stiahnutie v súbore kvet.frag.

SDF (signed distance function)

Jedným z možných spôsobov vyjadrenia, či bod leží v objekte, alebo mimo je SDF funkcia, ktorá vráti najkratšiu vzdialenosť od objektu ak bod leží mimo objektu, alebo záporné číslo ak je bod vo vnútri objektu.

Vyjadrenie SDF funkcie pre kruh je pomerne jednoduché:

float sdf_circle(in vec2 pixel, in vec2 center, in float radius)
{
    return distance(pixel, center) - radius;
}

Čierno-biely kruh s antialiasingom sa dá vykresliť pomocou nalsedujúceho kódu:

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Súradnice v rozsahu [-0.5, 0.5]
    vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);
    // Veľkosť pixelu vyjadrená v jednotkách súradníc
    float pixel_size = 1.0 / min(iResolution.x, iResolution.y);

    // Funkcia vzdialenosti
    float d = sdf_circle(uv, vec2(0.0), 0.4);

    // Farba popredia a pozadia
    vec3 color = mix(
        vec3(1.0),
        vec3(0.0),
        clamp(d * 1.0 / pixel_size, 0.0, 1.0) // Antialiasing
    );
    fragColor = vec4(color, 1.0);
}

Pre lepšiu vizualizáciu hodnoty funkcie urobím pár zmien v zobrazení. V prvom rade zmením farby pozadia a popredia:

// Farba popredia a pozadia
vec3 color = mix(
    vec3(0.45, 0.5, 0.7),
    vec3(0.7, 0.6, 0.4),
    clamp(d * 1.0 / pixel_size, 0.0, 1.0) // Antialiasing
);

fragColor = vec4(color, 1.0);

Ďalej pridávam biele orámovanie. To bude implementované funkciou mix, ktorá vráti aktuálnu farbu ak je posledný parameter nulový, bielu ak je 1 a mix ak je niekde medzi. Hrúbka čiary bude mať veľkosť 10 pixelov. Keďže máme funkciu vzdialenosti, na vykreslenie 5 pixelov hrubej čiary stačí vyfarbiť všetky body, ktoré majú absolútnu hodnotu vzdialenosti menšiu než 5 (teda do +5 z vonkajšej strany a -5 z vnútornej strany objektu.

// Farba popredia a pozadia
vec3 color = mix(
    vec3(0.45, 0.5, 0.7),
    vec3(0.7, 0.6, 0.4),
    clamp(d * 1.0 / pixel_size, 0.0, 1.0) // Antialiasing
);

// Orámovanie
color = mix(
    color,
    vec3(1.0),
    step(0.0, 5.0 * pixel_size - abs(d))
);

fragColor = vec4(color, 1.0);

Orámovaniu chýba antialiasing. Opraviť sa to dá napríklad vydelením vzdialenosti veľkosťou pixelu, čím sa vyráta vzdialenosť v pixeloch a tú orezať na hodnoty [0.0, 1.0], čím vznikne 1 pixel hrubé rozhranie, ktoré bude obsahovať mix farieb.

// Orámovanie
color = mix(
    color,
    vec3(1.0),
    clamp((5.0 * pixel_size - abs(d)) / pixel_size, 0.0, 1.0)
);

Zároveň by bolo vhodné nejakým spôsobom zobraziť vzdialenosť. Napríklad pomocou farebných prúžkov. Začnem jednoduchým periodickým znížením jasu o 30%.

Jas sa bude vypočítavať ako 70% + (0 až 30%). Hodnota útlmu bude rovná hodnote vzdialenosti za desatinnou čiarkou. Keďže vzdialenosť bude v rozsahu [-0.5, 0.5], teda celková vzdialenosť medzi okrajmi je 1.0 a chceme prúžkov viacej, bude sa vzdialenosť násobiť počtom prúžkov (strips).

const float strips = 10.0;

// …

// Farba popredia a pozadia
vec3 color = mix(
    vec3(0.45, 0.5, 0.7),
    vec3(0.7, 0.6, 0.4),
    clamp(d * 1.0 / pixel_size, 0.0, 1.0) // Antialiasing
);

// Prúžky
color *= 0.7 + fract(d * strips) * 0.3;

// Orámovanie
color = mix(
    color,
    vec3(1.0),
    clamp((5.0 * pixel_size - abs(d)) / pixel_size, 0.0, 1.0)
);

fragColor = vec4(color, 1.0);

Osobne by sa mi viac páčili prúžky, ktoré by mali len 2 farby namiesto gradientu.

Funkcia fract vráti hodnoty v rozsahu [0, 1]. Teoreticky by som mohol využiť funkciu step s hraničnou hodnotou 0.5 a dostal by som pekné prúžky, ale bez antialiasingu.

color *= 0.7 + step(0.5, fract(d * strips)) * 0.3;

Doteraz som pri antialiasingu využíval fakt, že funkcie mali hladký priebeh. Funkcia fract je iná, pretože má ostrý skok medzi 0 a 1. Bolo by vhodnejšie, keby sa ako medzné hodnoty nepoužívali 0 a 0.5, ale napríklad 0.25 a 0.75. Jednoduchý trik ako to dosiahnuť je odrátať od hodnoty fract 0.5, čím vnikne rozsah [-0.5, 0.5], z neho vypočítať absolútnu hodnotu a ako medznú hodnotu použiť 0.25.

color *= 0.7 + step(0.25, abs(fract(d * strips) - 0.5)) * 0.3;

Pretože sa využíva stredná časť funkcie fract nastáva zlom medzi prúžkami na hodnote 0.25. Zlom sa dá posunúť do pôvodnej podoby prirátaním konštanty 0.25.

color *= 0.7 + step(0.25, abs(fract(d * strips + 0.25) - 0.5)) * 0.3;

Teraz zostáva ešte vyriešiť problém s antialiasingom. Nasledujúci kód využíva využíva rovnaký trik na vykreslenie antialiasingu, ako bol použitý pri vykreslení kruhu.

color *= 0.7 + clamp((abs(fract(d * strips + 0.25) - 0.5) - 0.25) / pixel_size / strips, 0.0, 1.0) * 0.3;

Nakoniec len pre vizuálny efekt tieň a presvetlenie. Vnútorná časť objektu bude v blízkosti okraja presvetlená o 50% a vonkajšia v tieni s hustotou 80%.

const float strips = 20.0;


float sdf_circle(in vec2 pixel, in vec2 center, in float radius)
{
    return distance(pixel, center) - radius;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Súradnice v rozsahu [-0.5, 0.5]
    vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);
    // Veľkosť pixelu vyjadrená v jednotkách súradníc
    float pixel_size = 1.0 / min(iResolution.x, iResolution.y);

    // Funkcia vzdialenosti
    float d = sdf_circle(uv, vec2(0.0), 0.4);

    // Farba popredia a pozadia
    vec3 color = mix(
        vec3(0.45, 0.5, 0.7),
        vec3(0.7, 0.6, 0.4),
        clamp(d * 1.0 / pixel_size, 0.0, 1.0) // Antialiasing
    );

    // Prúžky
    color *= 0.7 + clamp((abs(fract(d * strips + 0.25) - 0.5) - 0.25) / pixel_size / strips, 0.0, 1.0) * 0.3;

    // Tiene
    color = mix(
        color,
        d > 0 ?
            mix(color, vec3(0.0), 0.8) :
            mix(color, vec3(1.0), 0.5),
        exp(-10.0 * abs(d))
    );

    // Orámovanie
    color = mix(
        color,
        vec3(1.0),
        clamp((5.0 * pixel_size - abs(d)) / pixel_size, 0.0, 1.0)
    );

    fragColor = vec4(color, 1.0);
}

Podobným spôsobom je možné vykresliť napríklad obdĺžnik.

float sdf_rect(in vec2 pixel, in vec2 start, in vec2 size)
{
    vec2 pix = pixel - start - size / 2.0;
    vec2 dist = abs(pix) - size;
    return length(max(dist, 0.0)) + min(max(dist.x, dist.y), 0.0);
}

// …

float d = sdf_rect(uv, vec2(-0.2, -0.1), vec2(0.4, 0.2));

Vykreslenie n-uholníka je možné napríklad týmto kódom (pôvodný kód je tu):

float sdf_ngon(in vec2 pixel, in int count, in vec2 center, in float radius)
{
    vec2 pix = pixel - center;
    float segment_angle_size = M_PI / float(count);
    float pixel_angle = atan(pix.x, pix.y);
    float repeat = mod(pixel_angle, segment_angle_size * 2.0) - segment_angle_size;
    float inradius = radius * cos(segment_angle_size);
    float circle = length(pix);
    float x = sin(repeat) * circle;
    float y = cos(repeat) * circle - inradius;

    float inside = min(y, 0.0);
    float corner = radius*sin(segment_angle_size);
    float outside = length(vec2(max(abs(x) - corner, 0.0), y)) * step(0.0, y);
    return inside + outside;
}

// …

float d = sdf_ngon(uv, 8, vec2(0.0, 0.0), 0.3);

Rovnaký užívateľ má zverejnenú funkciu pre vykreslenie hviezdy (kód):

float sdf_star(in vec2 pixel, in int count, in vec2 center, in float radius, in float depth)
{
    vec2 pix = pixel - center;

    float segment_angle_size = M_PI / float(count);

    float pixel_angle = atan(pix.x, pix.y);
    float repeat = abs(fract(pixel_angle/(segment_angle_size * 2.0) - 0.5) - 0.5)*(segment_angle_size * 2.0);
    float circle = length(pix);
    float x = sin(repeat)*circle;
    float y = cos(repeat)*circle - radius;
    float uv_rotation = segment_angle_size + depth;
    vec2 uv = cos(uv_rotation)*vec2(x, y) + sin(uv_rotation)*vec2(-y, x);

    float corner = radius*sin(segment_angle_size)/cos(depth);
    float inside = -length(vec2(max(uv.x - corner, 0.0), uv.y))*step(0.0, -uv.y);
    float outside = length(vec2(min(uv.x, 0.0), uv.y))*step(0.0, uv.y);

    return inside + outside;
}

float d = sdf_star(uv, 5, vec2(0.0, -0.05), 0.5, 0.6);

Medzi výhody SDF funkcií patrí napríklad možnosť jednoducho zaobliť rohy.

float rounded(in float dist, in float radius)
{
    return dist - radius;
}

// …

// Zaoblenie s polomerom 30px
float d = rounded(sdf_star(uv, 5, vec2(0.0, -0.05), 0.4, 0.6), 30.0 * pixel_size);

Jednoduchá je aj modifikácia plného tvaru na obrys.

float outline(in float dist, in float size)
{
    return abs(dist) - size;
}

// …

// Vykreslenie s hrúbkou 2 x 4 pixely
float d = outline(sdf_ngon(uv, 5, vec2(0.0, 0.0), 0.3), 4.0 * pixel_size);

Kompletný zdrojový kód je v súbore sdf.frag. Pekná zbierka SDF funkcií je dostupná na stránke iquilezles.org.

Transformácie

Veľmi často sa pri vykresľovaní používajú rôzne transformácie ako napríklad posun, zväčšenie, či rotácia. Prvý zdrojový kód vyzerá trochu monštrózne, ale nie je v ňom nič, čo by už nebolo použité v minulosti. V nasledujúcich príkladoch bude tento kód slúžiť ako kostra a meniť sa bude len kód na mieste komentára "Transformácia" vo funkcii mainImage.

#define M_PI 3.141592654


float sdf_circle(in vec2 pixel, in vec2 center, in float radius)
{
    return distance(pixel, center) - radius;
}

float sdf_rect(in vec2 pixel, in vec2 start, in vec2 size)
{
    vec2 pix = pixel - start - size / 2.0;
    vec2 dist = abs(pix) - size / 2.0;
    return length(max(dist, 0.0)) + min(max(dist.x, dist.y), 0.0);
}

float sdf_ngon(in vec2 pixel, in int count, in vec2 center, in float radius)
{
    vec2 pix = pixel - center;
    float segment_angle_size = M_PI / float(count);
    float pixel_angle = atan(pix.x, pix.y);
    float repeat = mod(pixel_angle, segment_angle_size * 2.0) - segment_angle_size;
    float inradius = radius * cos(segment_angle_size);
    float circle = length(pix);
    float x = sin(repeat) * circle;
    float y = cos(repeat) * circle - inradius;

    float inside = min(y, 0.0);
    float corner = radius*sin(segment_angle_size);
    float outside = length(vec2(max(abs(x) - corner, 0.0), y)) * step(0.0, y);
    return inside + outside;
}

float sdf_star(in vec2 pixel, in int count, in vec2 center, in float radius, in float depth)
{
    vec2 pix = pixel - center;

    float segment_angle_size = M_PI / float(count);

    float pixel_angle = atan(pix.x, pix.y);
    float repeat = abs(fract(pixel_angle/(segment_angle_size * 2.0) - 0.5) - 0.5)*(segment_angle_size * 2.0);
    float circle = length(pix);
    float x = sin(repeat)*circle;
    float y = cos(repeat)*circle - radius;
    float uv_rotation = segment_angle_size + depth;
    vec2 uv = cos(uv_rotation)*vec2(x, y) + sin(uv_rotation)*vec2(-y, x);

    float corner = radius*sin(segment_angle_size)/cos(depth);
    float inside = -length(vec2(max(uv.x - corner, 0.0), uv.y))*step(0.0, -uv.y);
    float outside = length(vec2(min(uv.x, 0.0), uv.y))*step(0.0, uv.y);

    return inside + outside;
}

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Súradnice v rozsahu [-0.5, 0.5]
    vec2 uv = (fragCoord.xy - iResolution.xy * 0.5) / min(iResolution.x, iResolution.y);

    // Tranformácia

    const vec2 start = vec2(-0.7, -0.5);
    const float shape_size = 0.2;

    if (uv.x < start.x || uv.x > -start.x || uv.y < start.y || uv.y > -start.y) {
        return;
    }

    int grid_x = int((uv.x - start.x) * (1.0 / shape_size));
    int grid_y = int((uv.y - start.y) * (1.0 / shape_size));
    int grid_index = grid_x + 7 * grid_y;
    int shape_index = grid_index % 4;

    vec2 tile_start = start + shape_size * vec2(float(grid_x), float(grid_y));

    float d;

    if (shape_index == 0) {
        d = sdf_circle(uv, tile_start + vec2(0.1, 0.1), 0.08);
    }
    else if (shape_index == 1) {
        vec2 rect_size = vec2(0.2 * float(grid_x + 1) / 7.0, 0.2 * float(grid_y + 1) / 7.0);
        d = sdf_rect(uv, tile_start + 0.5 * (vec2(shape_size) - rect_size), rect_size);
    }
    else if (shape_index == 2) {
        d = sdf_ngon(uv, grid_index / 4 + 3, tile_start + vec2(0.1, 0.1), 0.08);
    }
    else if (shape_index == 3) {
        d = sdf_star(uv, grid_index / 4 + 3, tile_start + vec2(0.1, 0.1), 0.08, float(grid_index) / 30.0);
    }

    if (d < 0.0) {
        fragColor = vec4(1.0);
    }
}

Najjednoduchšou transformáciou je posun. Napríklad pre posunutie objektov o 0.2, 0.0 (0.2 doprava) stačí odrátať (0.2, 0.0) od súradníc.

// Presun
const vec2 move = vec2(0.2, 0.0);
uv -= move;

Zväčšenie je podobne jednoduché. Stačí súradnice vydeliť žiadanou hodnotu zoomu.

// Presun
const vec2 move = vec2(0.2, 0.0);
uv -= move;
// Zoom
const float zoom = 2.0;
uv /= zoom;

Nakoniec pre otočenie sa súradnice upravia pomocou vzťahu x' = x * cos(θ) + y * sin(θ) a y' = -x * sin(θ) + y * sin(θ).

// Presun
const vec2 move = vec2(0.2, 0.0);
uv -= move;
// Zoom
const float zoom = 2.0;
uv /= zoom;
// Otočenie
const float angle = M_PI / 8.0;
uv = vec2(
    uv.x * cos(angle) + uv.y * sin(angle),
    -uv.x * sin(angle) + uv.y * cos(angle)
);

Transformácia v príklade prebiehala v niekoľkých krokoch. Obyčajne sa všetky afinné transformácie implementujú ako jediné násobenie transformačnou maticou.

Nasledujúci kód je ekvivalentný predchádzajúcim transformáciám, ale všetky kroky sú zlúčené do jedinej transformácie. Celý výpočet transformačnej matice sa vykonáva počas kompilácie. Počas behu sa vykonáva už len násobenie.

// Presun
const vec2 move = vec2(0.2, 0.0);
const mat3 move_matrix = mat3(
    vec3(1.0, 0.0, -move.x),
    vec3(0.0, 1.0, -move.y),
    vec3(0.0, 0.0, 1.0)
);
// Zoom
const float zoom = 2.0;
const mat3 zoom_matrix = mat3(
    vec3(1.0/zoom, 0.0, 0.0),
    vec3(0.0, 1.0/zoom, 0.0),
    vec3(0.0, 0.0, 1.0)
);
// Otočenie
const float angle = M_PI / 8.0;
const mat3 rotate_matrix = mat3(
    vec3(cos(angle), sin(angle), 0.0),
    vec3(-sin(angle), cos(angle), 0.0),
    vec3(0.0, 0.0, 1.0)
);
// Zložená transformácia
const mat3 transform = move_matrix * zoom_matrix * rotate_matrix;

// Transformácia (k vektoru uv sa musí pridať tretí prvok s hodnotou 1)
uv = (vec3(uv, 1.0) * transform).xy;

Výsledný kód je v súbore transform.frag.

Vykreslenie matematickej funkcie

V ďalšom príklade by som chcel ukázať vykreslenie funkcie. Vybral som si peknú hladkú funkciu sínus. Na začiatok si definujem rôzne konštanty. V prvom rade je to konštanta pí, ktorú budem potrebovať, aby som vykreslil presne celú periódu. Ďalšie konštanty obmedzujú oblasť, ktorú chcem vykresliť.

#define M_PI 3.1415926535897932384626433832795

#define MIN_X 0.0
#define MAX_X (M_PI * 2.0)
#define MIN_Y (-1.1)
#define MAX_Y 1.1

Funkcia bude mať názov fn. Jediný vstupný argument bude mať typ float. Návratová hodnotu tiež float. Telo funkcie tvorí jediné volanie sínusu.

float fn(float x) {
    return sin(x);
}

Hlavná funkcia normalizuje koordináty podľa minimálnej a maximálnej hodnoty, vypočíta hodnotu matematickej funkcie a vykreslí bielou farbou všetky pixely, ktoré na y osi prekročia hodnotu funkcie v danom bode.

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Normalizácia súradnic podľa MIN/MAX_X/Y
    vec2 uv = vec2(
        MIN_X + (MAX_X - MIN_X) * (fragCoord.x / iResolution.x),
        MIN_Y + (MAX_Y - MIN_Y) * (fragCoord.y / iResolution.y));

    // Výpočet y pre x
    float y = fn(uv.x);

    // Vykreslenie bielou farbou ak hodnota funkcie prekročí hodnotu
    // koordinátu y
    float color = step(y, uv.y);
    fragColor = vec4(vec3(color), 1.0);
}

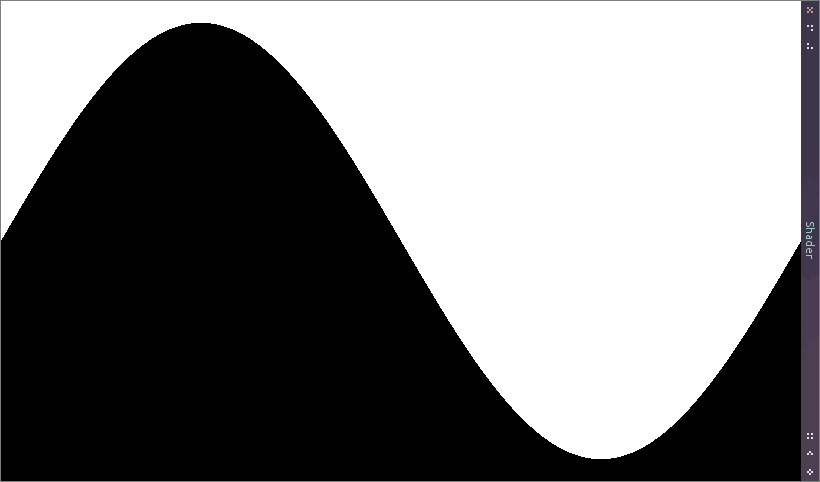
Funkcie sú obyčajne vykreslené pomocou čiar. Skúsme teda upraviť funkciu mainImage tak, aby vykreslila čiaru.

void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
    // Normalizácia súradnic podľa MIN/MAX_X/Y
    vec2 uv = vec2(
        MIN_X + (MAX_X - MIN_X) * (fragCoord.x / iResolution.x),
        MIN_Y + (MAX_Y - MIN_Y) * (fragCoord.y / iResolution.y));

    // Výpočet y pre x
    float y = fn(uv.x);
    // Derivácia y podľa x (hodnota y v nasledujúcom pixeli vpravo)
    float dy = dFdx(y);
    // Kladná hodnota rozdielu y v nasledujúcom pixeli
    float absDy = abs(dy);

    // Uloženie rozsahu od aktuálnej hodnoty y po nasledujúcu hodnotu
    float minY = min(y + dy, y);
    float maxY = minY + absDy;

    // Všetky pixely s hodnotou vyššou než dolná hranica y a zároveň nižšou než
    // horná hranica y budú mať bielu farbu
    float color = step(minY, uv.y) * (1.0 - step(maxY, uv.y));

    fragColor = vec4(vec3(color), 1.0);
}

V predchádzajúcom texte som spomínal, že zo shaderu nie je možné pristupovať k ostatným pixelom. To síce platí, okrem jednej výnimky - je možné získať zmenu voči susedným bunkám (derivácia podľa osi x a y). Keďže je možné zistiť zmenu voči susednému pixelu, je možné doplniť zvyšné prázdne body čiary.

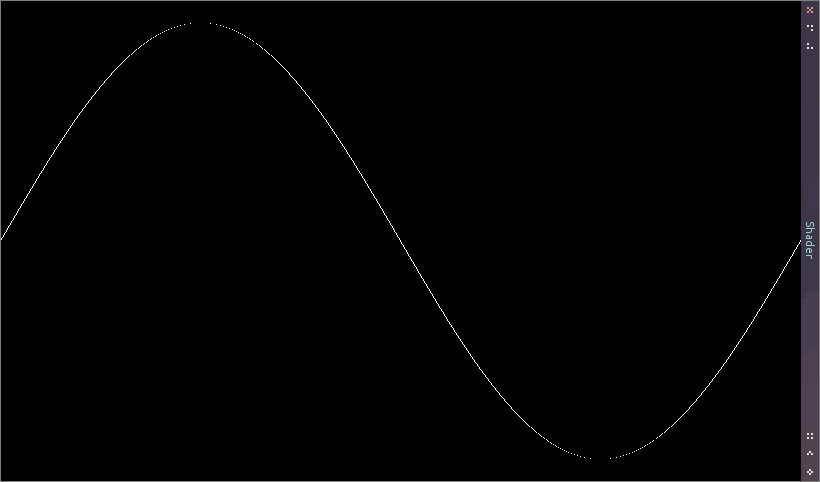
Vykreslenie nie je úplne dokonalé, pretože hodnota dy nadobúda v niektorých častiach funkcie hodnotu menšiu než jeden pixel. Nie je až tak ťažké túto situáciu ošetriť. Stačí prirátať 1 pixel k maximálnej hodnote y.

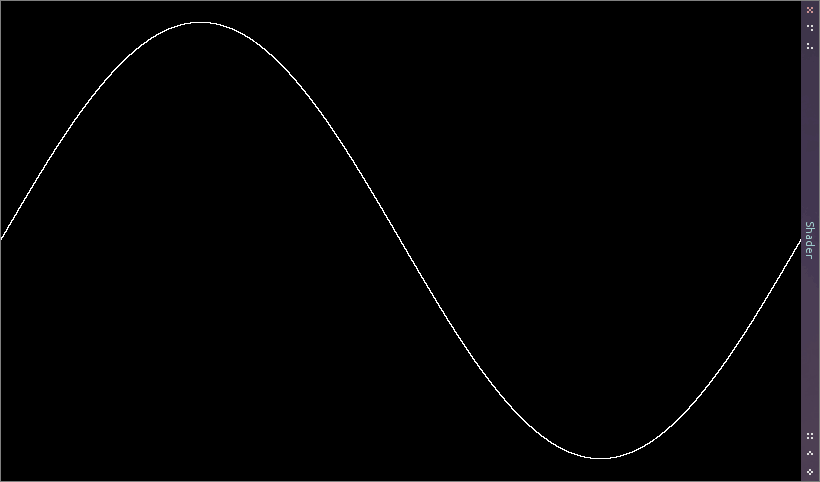
Bolo by možné vykreslenie ešte vylepšiť? Samozrejme! Napríklad antialiasingom. Nie je to nič zložité, stačí sa pri výpočte farby pohrať s funkciou smoothstep.

float color =
    smoothstep(minY - absDy - pixelHeight * 0.5, minY, uv.y) *
    (1.0 - smoothstep(maxY, maxY + absDy + pixelHeight * 0.5, uv.y));

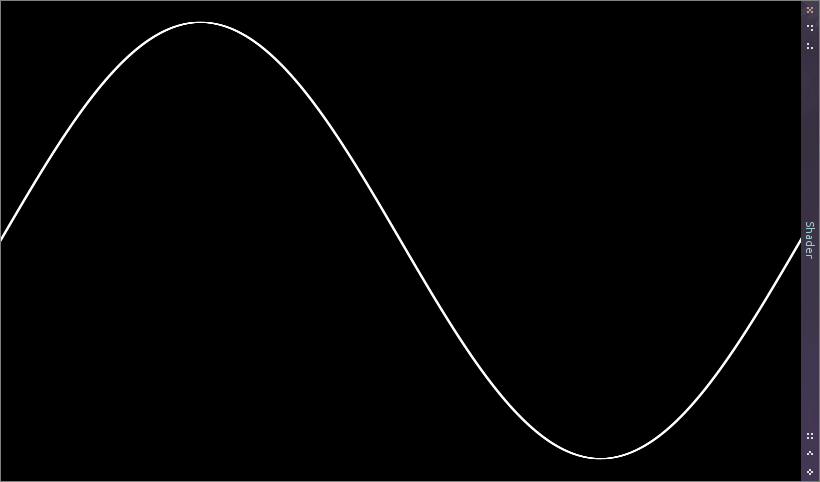
Výpočet funkcie vyzerá na mojom notebooku korektne. Netreba sa však spoliehať na presnosť výpočtu. Grafické karty sú v prvom rade navrhnuté pre vysoký výkon. Presnosť výpočtu ide tak trochu bokom.

Niektorí pamätníci si možno pamätajú FDIV bug v procesoroch Intel. Vďaka nesprávnemu výpočtu sa stal častým terčom vtipov.

Popis rozhovoru medzi Pentiom a Motorolou:
Motorola (pomaly): Koľko je 2 x 2?
Pentium (rýchlo): 8.
Motorola (pomaly): To je ale nesprávne. 2 x 2 sú predsa 4.
Pentium (rýchlo): Nesprávne, ale rýchlo.

Počas dlhých zimných večerov som sa trocha hral s generovaním zvuku cez OpenGL shader. Zo začiatku to išlo celkom dobre, ale po pár sekundách sa zvuk zmenil skokovo na nepríjemnú cirkulárku. Pri tejto príležitosti som si právne napísal program na vykreslenie priebehu funkcie. Na nasledujúcom obrázku je priebeh funkcie sínus na Intel HD 3000 po prekročení hodnoty 8190 na osi x.

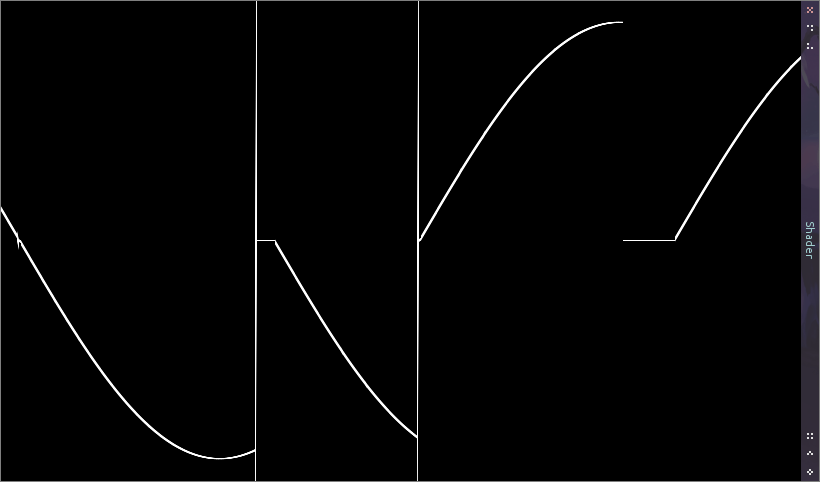
Obrázok 29: Sínus na intel HD 3000 pre x začínajúce v 8190

Implementácia sínusu na GPU intel je tak zlá, že Mesa musí implementovať hack INTEL_PRECISE_TRIG, ktorý orezáva hodnoty sínusu do intervalu [-1, 1]. Vážne na Inteli lieta sínus mimo tento interval. Mimochodom INTEL_PRECISE_TRIG rieši len hodnoty mimo intervalu, nie rozbitý sínus pre väčšie čísla.

Zdrojový kód je dostupný v súbore sin.frag.

Na záver prikladám pár pekných shaderov, ktoré využívajú 2D grafiku. Nasledujúca časť sa bude venovať 3D grafike metódou ray tracingu.